4. 基本動定格荷重と疲れ寿命
転がり軸受の負荷能力を表わす基本動定格荷重とは、外輪静止状態にて内輪を100万回転できる方向と大きさが変化しない荷重です。
そして、荷重を負荷しながら、回転すると外輪または内輪の軌道面と転動体の転動面は繰り返し荷重を受けるため、材料の疲れによるうろこ状の損傷(フレーキングと呼びます)が軌道面または転動面に現れます。この損傷が現れるまでの総回転数が転がり疲れ寿命であり、単に軸受寿命と呼ぶこともあります。
軸受寿命
音、振動または、トルクが大きくなったので交換、軸受温度が高くなったので交換など、ユーザーやアプリケーションによって、軸受寿命の考え方は様々です。これらの軸受寿命は、経験または、統計学に基づく計算で予測されます。

転がり疲れ寿命
軸受が荷重を受けて回転すると、内外輪の軌道面と転動体の転動面は、繰返し荷重を受け、内部応力が発生します。
このため、ついには材料の疲れによって、フレーキングと呼ばれる うろこ状の損傷が軌道面または、転動面(主に内輪軌道面)に現れます。
この損傷が生じるまでの総回転数を転がり疲れ寿命と呼びます。


内輪軌道面の剥離例
転がり疲れ寿命のばらつき
転がり疲れ寿命は、寸法 構造 材料 処理熱 加工方法 などを同じにした数多くの軸受を同一条件で運転しても、下図のように、相当大きなばらつきがあります。これは、材料の疲れそのものに本質的な ばらつきがあるためです。
よって、この寿命の ばらつき を統計的現象ととして取扱い、次のように定義された基本定格寿命を用います。
基本定格寿命(L10) = 一群の同一軸受を、同一条件で個々に回転させたとき、そのうちの90%の軸受が転がり疲れによるフレーキングを起こすことなく回転できる総回転数
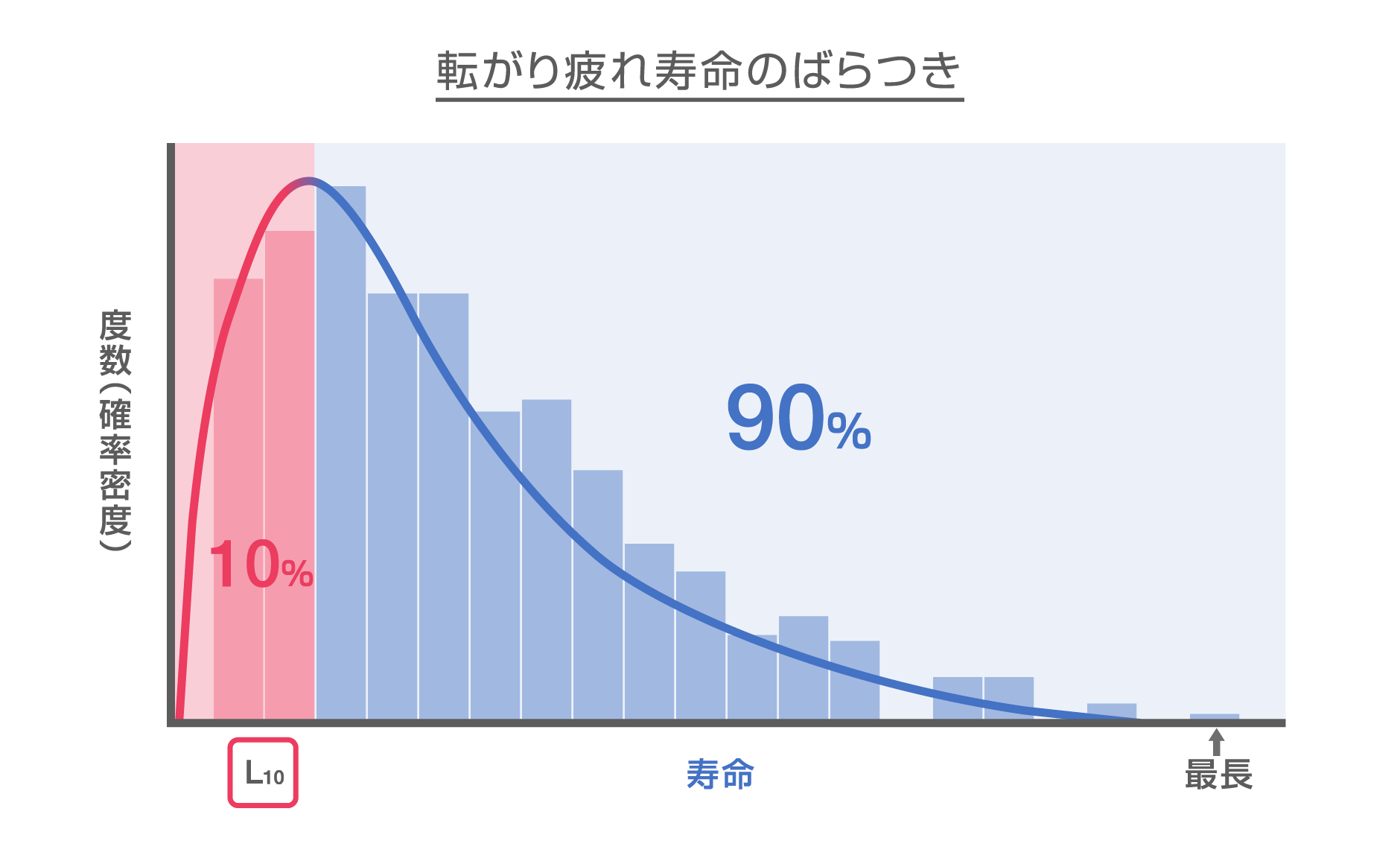
基本定格寿命 L10
同一名番軸受を同一条件で個々に回転させた時、その内の90%の軸受が転がり疲れによるフレーキング(はくり)を起こさず、回転できる総回転数を基本定格寿命(L10)と呼びます。
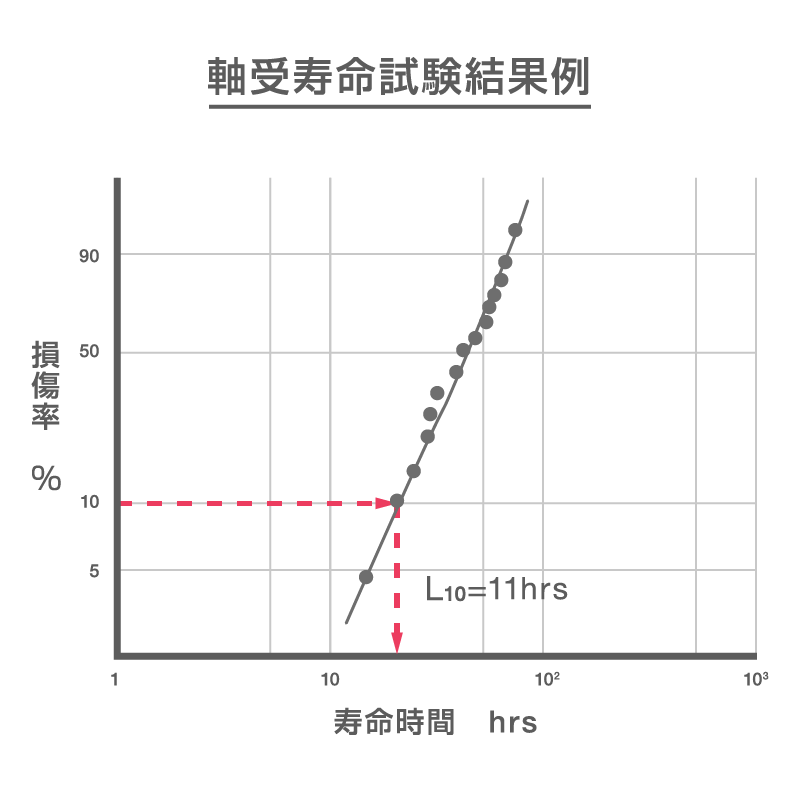
- 左図は軸受寿命試験結果を基に時間と不信頼度(損傷率)を直線近似で可視化する方法であり、ワイブルプロットと呼ばれます。
- ワイブルプロットは、信頼性試験によって得られたデータがワイブル分布(※)に従うかどうかの判定と、ワイブル分布のパラメータを求めるために、片対数のX軸に時間を、Y軸に累積故障率(損傷率)を記述したものです。
※物体の強度を統計的に記述するための「確率分布」です。
基本動定格荷重
定義:内輪回転、外輪静止条件下で、100万回(106)、回転させた際、定格疲れ寿命(10%の故障率または、90%の信頼度係数)を確保できる方向と大きさが変動しない荷重。
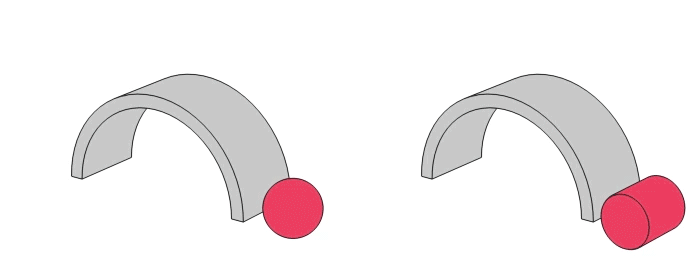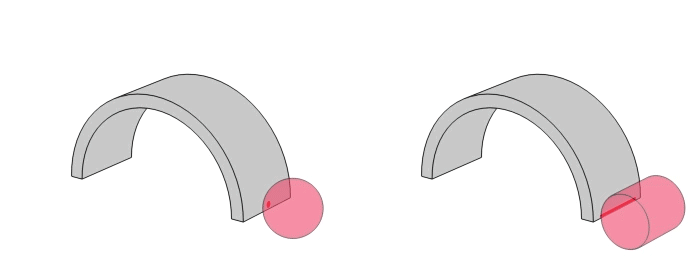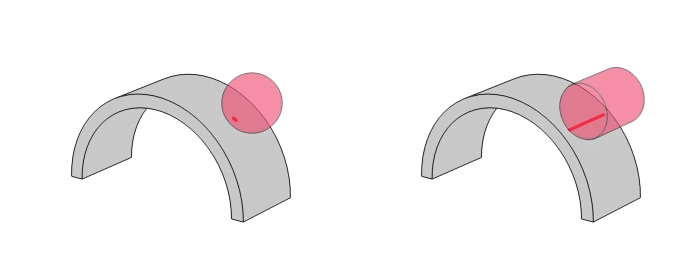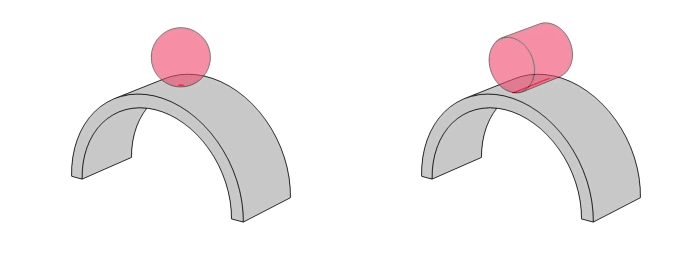
点接触
点接触は軽荷重低トルクおよび高速向き
線接触
線接触は重荷重低速向き
L10 =(C/P)3 玉軸受の場合
=(C/P)10/3 ころ軸受の場合
ここで
L10:信頼度90%の基本定格寿命 [X106回転]
C:基本動定格荷重[N]
“C”は、ラジアル軸受の場合“Cr”、スラスト軸受の場合“Ca”と表します。
P:軸受(に掛かる)荷重(等価荷重)[N]
“P”は、ラジアル方向荷重の場合“Pr”、アキシアル(スラスト)方向荷重の場合“Pa”と表します。
荷重の大きさと寿命
転がり軸受の基本動定格荷重C、軸受荷重Pと基本定格疲れ寿命L10との間には、次の関係があります。
基本動定格荷重C ⇒ 100万回転の寿命を与える一定荷重
玉軸受では L10=(C/P)3
ころ軸受では L10=(C/P)10/3
L10:基本定格寿命(×106回転)
P:軸受荷重(動等価荷重)(N)
C:基本動定格荷重(N)
基本定格疲れ寿命は時間で表わしたほうが便利です。
軸受の基本定格疲れ寿命と回転速度との間には、次のような関係があります。
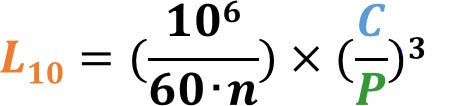
玉軸受
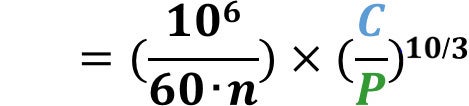
ころ軸受
ここで
L10:基本定格寿命(h)
n:回転数(min-1)

玉軸受:荷重が半分になると、寿命は8倍
ころ軸受:荷重が半分になると、寿命は10倍
