ボールねじ送り系を対象とした軸力維持のための状態安定化機構の基本機能とモデル化
2026年1月
産業機械事業本部 産業機械技術総合開発センター 新井 覚
技術開発本部 デジタルツイン推進室 竹之内 優志
技術開発本部 デジタルツイン推進室 本多 信太郎
技術開発本部 コア技術研究開発センター 谷 翔太

本稿は、日本機械学会の学術誌に掲載された以下の論文を同学会からの転載許諾を受け掲載したものである。
Satoru ARAI, Yushi TAKENOUCHI, Shintaro HONDA and Shota TANI, Foundational development, modeling and configuration of state stabilizing mechanism to maintain axial tension in ball screw feed drive systems, Journal of Advanced Mechanical Design, Systems, and Manufacturing, Vol.19, No.1 (2025), pp.1-18. DOI: 10.1299/jamdsm.2025jamdsm0008
1. 緒言
切削や研削などの除去加工に使用される工作機械では、工具とワークの間の相対位置関係を保証する観点から、静的かつ動的なコンプライアンスに着目して制御指令による変位の誤差を最小化するように設計が行われる。
コンプライアンス低減に関しては、工作機械の構造的な形態はもちろんのこと、各構成要素に加えて接触部における機械特性に対する検討が必要になる(清水他、2005;稲垣他、2011)。機械加工の分野においては、特にこのコンプライアンスが、構成部位における発熱ならびに動的挙動の影響を顕著に受けることが知られており、それに対する様々な理論的考察や実践的改善策が提案されてきた(Weck、1984;Inasaki、2004;Arai他、2009;Altintas他、2011)。
工作機械の送り系においても、熱ならびに動的挙動は加工精度の高度化や生産性の向上に直接的に影響を与える重要な因子である(Altintas他、2011)。しかしながら発熱や熱の流れに絡む現象は、CAE解析が普及した今日にあっても完全に現象を数値モデル化できるとは言い難く、設計段階において普遍的に確立された現象把握手段があるわけではない(Mayr他、2012)。結果として実機上でのトライ・アンド・エラーを踏まえた対処がなされる場合が多く、このことが工作機械ごとの機能のばらつきや経時劣化の相違を生む要因となっている。
図1は、立形マシニングセンタ上におけるボールねじ送り系の構成例を示したものである。マシニングセンタや旋盤などに実装されるボールねじ送り系において発熱の影響を見てみると、モータ、ナット、軸受などで生じた発熱は、機台、ねじ軸、テーブル、案内などを通り構造体各部へ伝播するほか、大気中へ放出される。これらの熱の流れが工作機械の構造体内や周囲の雰囲気中で安定し、機械の熱変形が定常化した状態になるまでには、工作機械自体の暖機運転などに相応の時間を要することになる。そのため特に高精度な機械加工が要求される場合には、ボールねじのねじ軸の軸芯部に貫通穴を設け冷媒を流動させることで冷却し線膨張を抑制したり(二宮、宮口、1997)、ナットにジャケットを構成して冷却したりするほか(水口他、2015)、工作機械が設置された環境の雰囲気を安定化するために恒温室を整備して工作機械が設置された環境の雰囲気を変化しにくくするなどの対処が取られる(Bryan、1990)。しかしながらこれらの対処方法は、構成要素の冷却や設置環境の室温安定のために二次的なエネルギーの投入を伴うほか、加工精度や品質の要求に見合うために大規模な設備投資を必要とする場合もあるため、その適用が高付加価値の用途向けに限られてきた。
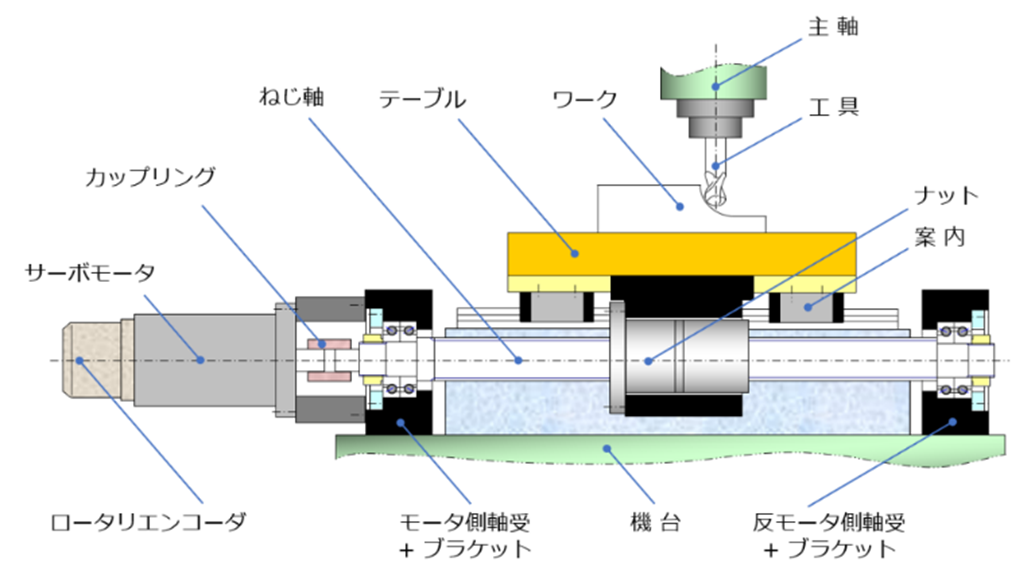
図1 立形マシニングセンタ上におけるボールねじ送り系の構成例
工作機械の各部での発熱によるボールねじ送り系の変形のうち、加工精度に対して直接的に大きな影響を及ぼす因子は、ねじ軸の伸びである(横山他、2006)。代表的な発熱体であるナットに加えてねじ軸を支持する軸受などから発生した熱は、ねじ軸に流れ込み線膨張をもたらすことでボールねじの位置決め精度を著しく低下させる。
これに加えてねじ軸の継続的伸長は、送り系の機械特性にも変化をもたらす。図2は、ねじ軸の反モータ側に予張力を付与した軸受支持構造の一例を示したものである。この例の場合DB組み合わせの反モータ側軸受部には、軸受部における潤滑状態や動定格荷重を考慮して通常3ºC分程度の線膨張に相当するねじ軸長の伸びを与える予張力が軸方向荷重として与えられる。ねじ軸左端に配置されたモータ側軸受が図1と同様に構造上の基準となる固定支持の構成であったとすると、反モータ側軸受側でも予張力が付与されることによりある程度の軸方向剛性を担保できるようになる(二宮、1978)。
このような構成においてねじ軸が発熱の影響により線膨張すると、反モータ側軸受はねじ軸の伸びに伴って一体的に右方向へ移動することになる。しかし反モータ側軸受部には予張力が付与されているため、温度上昇3ºC分までの線膨張約36 μm/m)に対しては、ねじ軸に軸力が掛り剛性を付与することが可能になる。すなわち、予張力を与えたねじ軸の支持構造の採用には、限られた温度条件範囲ではあるもののねじ軸の線膨張を許容しつつ軸方向剛性も持ち、発熱に対してロバスト性を高くできるメリットがある。
一方でねじ軸の右方向への伸びが大きくなり、ねじ軸に付与された予張力が作用しなくなるほど顕著になると、反モータ側軸受部の左側にある軸受の外輪左端面は機台に固定されたハウジングに接触しない状態になる(図2の右図では、ねじ軸の伸びを誇張して表現している)。これにより反モータ側軸受部に軸力が作用しなくなることから、この部位では軸方向荷重を支持できない状況となる。このような一連の変化はボールねじ送り系に軸方向剛性の低下をもたらし、それがサーボ系における共振点の低下に直結する。結果として工具とワークが接触する加工点においても相互の接触状態を変化させる遠因となり、振動や音の発生、加工品位の低下、品質のばらつきを誘発するため、この種の軸受支持構造を採用する際のデメリットとなっていた。
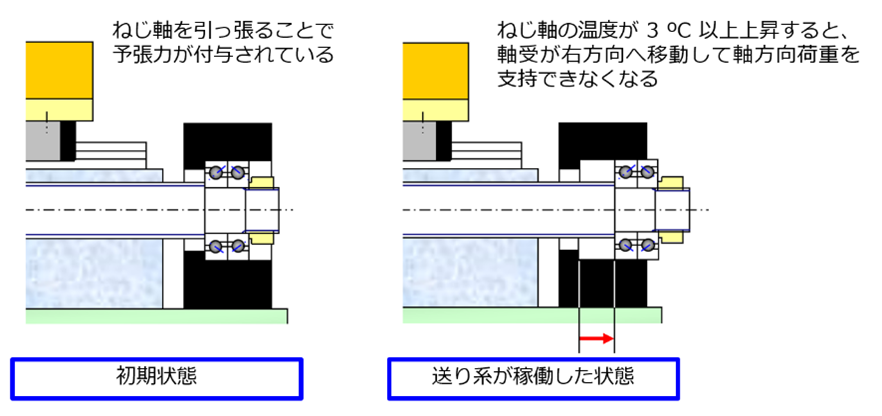
図2 反モータ側軸受に予張力を付与した軸受支持構造の一例とねじ軸伸長時の状態変化
経時変化を伴う上述の不安定な現象は、長年製造現場において属人的なスキルに依存した調整などの取り扱いを必要としてきた。具体的には、対象となる工作機械の現場担当者、すなわち日常的に設備に関与し特有のクセを熟知した作業者が加工点へのクーラントの掛け方を変化させたり、加工条件(加速度・速度・工具の回転速度、工具交換時期の設定 etc.)を低下させるなどの応急的処置で対応するほか、制御系に通じた生産技術者が専門知識にもとづいてサーボ系のゲイン調整を行う対処療法で当座の課題が改善され、これらが日々の製造現場におけるものづくりの維持に多大な貢献を果たしてきたと言える。
労働人口の減少に伴う工場の省人化や環境負荷の削減が急務となっている今日、エネルギー消費を削減しつつものづくりの高度自動化を実現するためには、このような設備や環境に依存する不安定な現象の発生を防ぎ、人や環境に依存した調整に対する抜本的措置を施すことが避けては通れない状況にある。
本研究ではボールねじ送り系のこのような課題に対して、発熱によりねじ軸が線膨張した場合であっても、安定的に軸力を維持し得る状態安定化機構(State stabilizing mechanism to maintain axial tension:以下SSMとする)を開発した。本稿では、本機構のしくみ、機能の基本となる内圧の発生モデルならびにそれにもとづく計算結果の妥当性について述べるとともに、ボールねじ送り系を構成する際に本機構の仕様を決定するためのプロセスを提案する。
2. ボールねじ送り系の状態安定化機構の構成と機能の検討方法
2.1 ボールねじ送り系の状態安定化機構の構成
図3(a)は、代表的な切削加工用の工作機械であるマシニングセンタ上の水平方向に配置されたボールねじ送り系において、ねじ軸の反モータ側軸端部にSSMを取り付けた構成例を示したものである。なお、 ここでは、モータ側軸受部は軸方向に対して位置の変わらない固定支持状態を前提としている。
図3(b)には、ねじ軸が発熱により伸長時した際、図3(a)の構成に取り付けられたSSMの内部において生じる動きを示している。SSMは、大きく分けてピストンとシリンダのふたつの部材により構成されている。シリンダは軸方向に可動である一方、ピストンに対しては相対的に回転しないように案内部を介して連結されている。図3(b)の例では、ピストンはブラケットを経て機台に固定され、シリンダはねじ軸を支持する反モータ側軸受と一体的にねじ軸に組み付けられている。
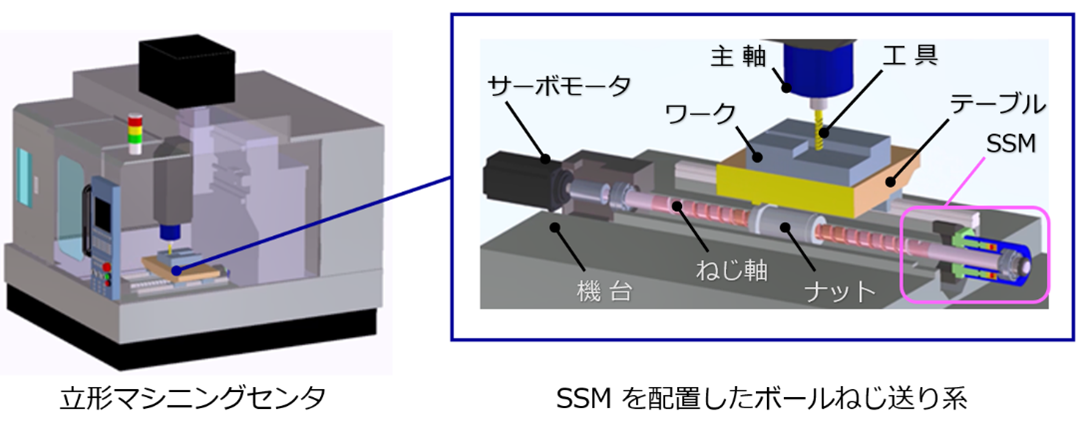
(a) マシニングセンタ上におけるボールねじ送り系の構成とSSMの配置例(カットモデル)
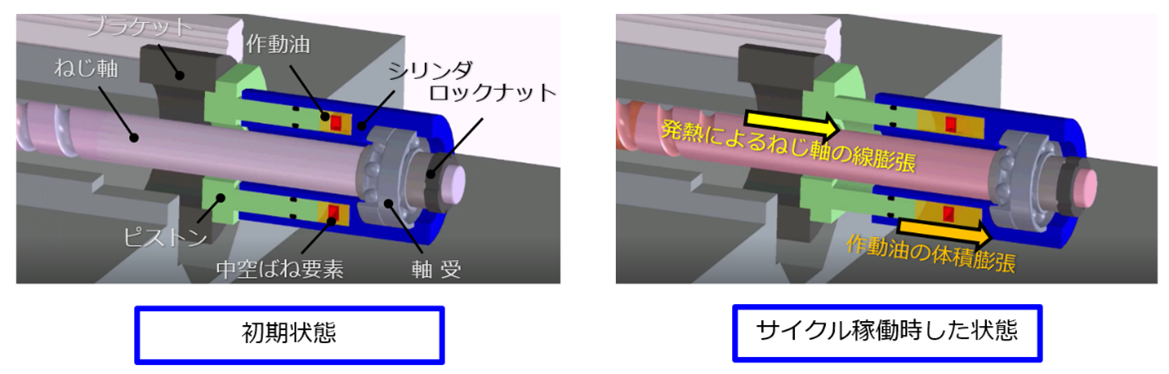
(b) ねじ軸が発熱により伸長した際のSSM内部の動き(カットモデル)
図3 マシニングセンタ上におけるSSMの配置と内部の動き
ピストンとシリンダの勘合部は、適切なシール構造を伴って隙間がないように適量の作動油で満たされている。ここでは、この作動油が封入された領域を圧力室と呼ぶものとする。上述の方法でねじ軸に対してロックナットを締め付けると、ねじ軸がSSMの中心部を貫通していることから、圧力室にはピストンとシリンダにより軸方向に圧縮する力が印可され内圧が発生する。これによりボールねじ送り系としては、ねじ軸において引張りの軸力が付与された状態になる。
本設定においてボールねじ送り系が加工サイクルで稼働したとき、ねじ軸はナットなどの発熱に伴って図3(b)のように右側へ線膨張することになる。この際、SSMを構成するシリンダもねじ軸と一体で移動するため、圧力室内では作動油により生じていた内圧が徐々に低下する。
一方でねじ軸の回転を支持する反モータ側軸受においては、送り系のサイクル稼働に伴って発熱を生じる。この熱はシリンダ部材内を通って圧力室にも伝わるため、圧力室内に封入された作動油に温度上昇をもたらす。本現象は、特に作動油の顕著な膨張を誘発するため、圧力室内において内圧を上昇させ軸方向の張力を高めることになる。
SSMの圧力室内において予圧の減少と内圧の上昇という相反するふたつの現象を考えるとき、これらの差により生み出された張力の変化が相殺するかたちでねじ軸の線膨張に追従できれば、ねじ軸に作用する軸力を安定的に維持することが可能になる。しかしながらこのような現象は、送り系の構成、加工サイクル、設置環境などの影響を受けることが予想され、適用にあたっては綿密な検討が必要になると考えられる。そこで本研究では、圧力室内における内圧変動の感度を軽減するために作動油中に図3(b)に示す中空ばね要素を内包させることとした。中空ばね要素は、作動油に比べて相対的に柔らかく構成されている。従って作動油の過度な熱膨張時には中空ばね要素が圧縮され、その体積が減少した領域に作動油の膨張分を受け入れることができる。加えて本構成では、圧力室の体積が収縮した際においても中空ばね要素に付与された圧力が圧力室内の内圧減少の低減に効果を発揮することが期待できる。
上述したように熱的および力学的観点で見ると、SSMは反モータ側軸受で発生した熱を圧力室で回収しつつ、これを活用してねじ軸に作用する軸力を一定に保つ『エネルギーの循環機構』として機能していることがわかる。
図4は、このエネルギー循環を図に示したものである。軸受で発生する熱は、SSMを機能させるエネルギー源である。SSMは、このエネルギーをねじ軸支持構造における力学特性の継続的安定化に寄与する仕事に変換するためのアイテムとみなせる。すなわち軸受から発生する熱エネルギーは、圧力室内に封入された作動油の温度上昇さらには体積膨張に寄与し、SSMが軸方向に伸長する原動力になる。このとき拡張した圧力室で発生する内圧による張力がねじ軸に当初から作用している軸力に近い状態であり続ければ、軸受に作用する荷重および発生する熱は安定的に維持され、圧力室に供給される熱量も一貫性を保ち続けることができる。このように安定して発生する熱量は、圧力室内の作動油の体積維持に直接的に貢献する。このループが継続して適切な状態に維持されるように圧力室を設計できれば、外部から何かしらの二次的なエネルギーを供給しなくても、SSMユニットのみで自律的に送り系の力学的な状態を安定化できるようになると考えられる。
2.2では、この『エネルギーの循環機構』が成立するボールねじ送り系の構成を実現させるためにSSMの圧力室で発生する内圧をモデル化したうえで、実践的に張力を計算する方法について述べる。
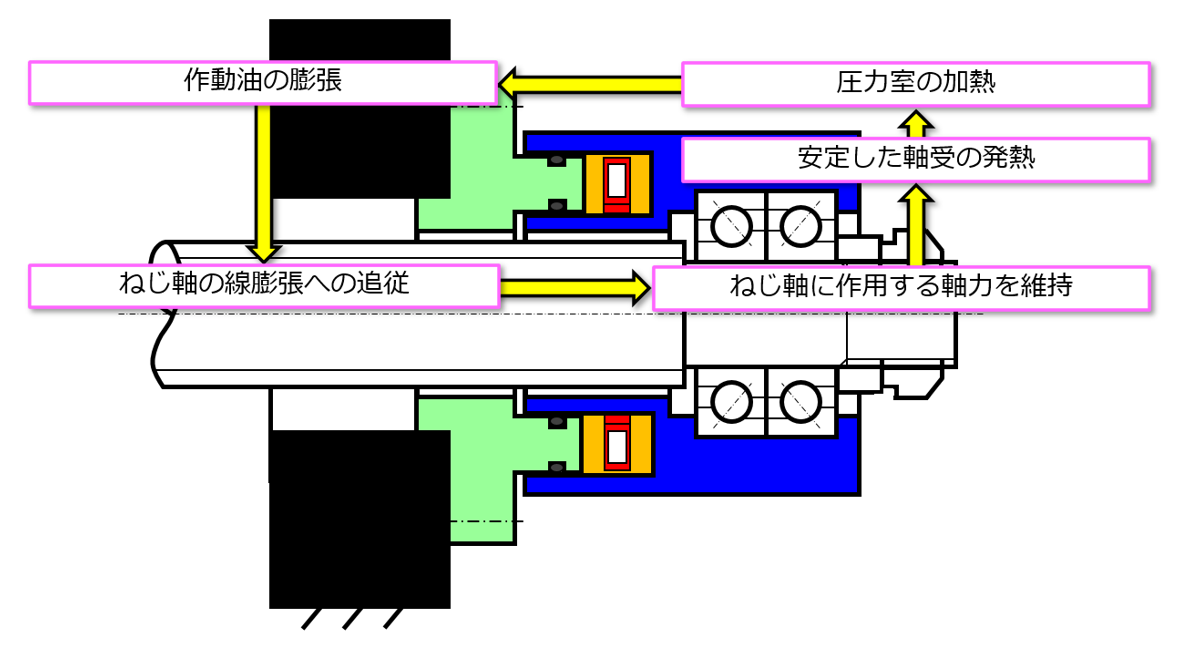
図4 熱的および力学的観点から見たSSM内でのエネルギーの循環
2.2 圧力室の内圧により発生する張力の導出方法
図5にSSM内部に設置された圧力室で発生する内圧による張力を導出するために考案したアルゴリズムを示す。
従来、ボールねじ送り系の発熱およびねじ軸の伸びに関しては、その現象モデルの立案を目的として様々な研究がなされてきた(垣野他、1988;小渕他、1987;千田、森脇、2006)。しかしこれらはいずれも実体のあるボールねじ送り系から発熱にかかわるパラメータを実験的に同定したうえでモデルに代入しシステム全体の解析を実施することを前提としたものであった。そのため、工作機械の構造、加工サイクル、環境設定まで含めたシステム全体を汎用的に解析して、その結果を設計に反映させることは依然として難しいのが実状であった。
これに対して本研究で提案する手法は、ねじ軸に作用する軸力を一定に保つことでボールねじ送り系の力学特性を継続的に安定化させるプロセスを構築することにフォーカスしている点に特徴がある。すなわち軸力維持の要となるSSMの圧力室内の内圧をモデル化するに際しては、ボールねじ送り系全体を対象とするのではなく、作動油や中空ばね要素の物性値・力学特性・体積、さらには時間ごとの圧力室内に封入された作動油の温度および圧力室内の体積を入力値とすることで圧力室内の内圧を求めSSMが生み出す張力に換算するアルゴリズムを構築している。
この際に必要となる作動油の温度ならびにねじ軸の伸びについては、予圧を付与した軸受をねじ軸の伸びに追従できる構造で支持した予備実験から求めるプロセスを考案した。
図6は、この予備実験においてねじ軸の伸びを測定する側の力学的構成の例を示したものである。提案する方法では、まず図6に示すように軸方向に可動な構成でSSMの圧力室内を大気に開放した状態で取り付けたボールねじ送り系を設定する。この送り系を対象として加工サイクル稼働させた予備実験において、ねじ軸がナットや軸受などの発熱に応じて素直にねじ軸方向へ伸びる状況を設定した際のねじ軸自身の伸び量ならびに圧力室の温度の時間履歴を求める。予備実験から導出された時間ごとのねじ軸の伸びは、図5に示す通り内圧の計算に直接用いることができる。その一方で作動油の温度については、圧力室に対応する位置で温度を測定しこれを実質的な相当値として用いることとした。
なお作動油や中空ばね要素の材料物性・力学特性・体積については、別途圧力室を構成するうえで基本となる構成仕様パラメータとして設定しておき、圧力室の内圧計算に適用した。
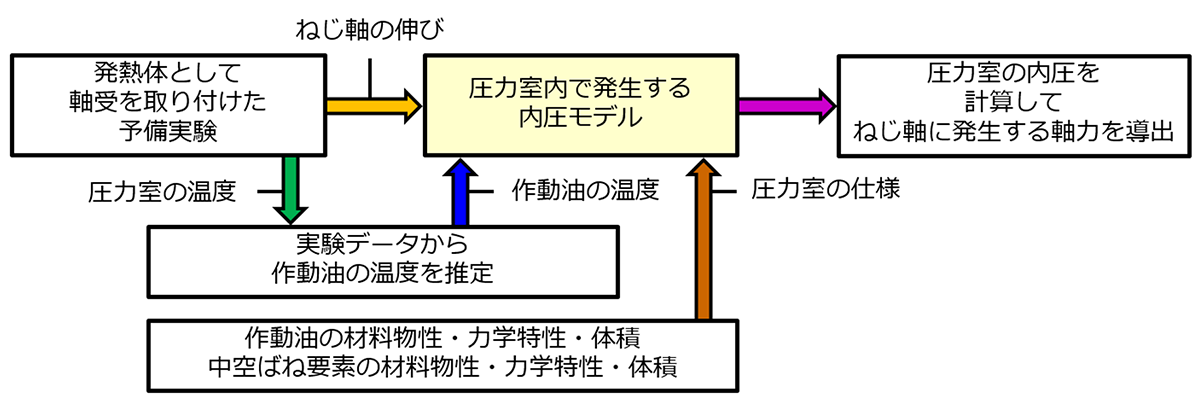
図5 SSM内部の圧力室で発生する内圧による張力を導出するアルゴリズム
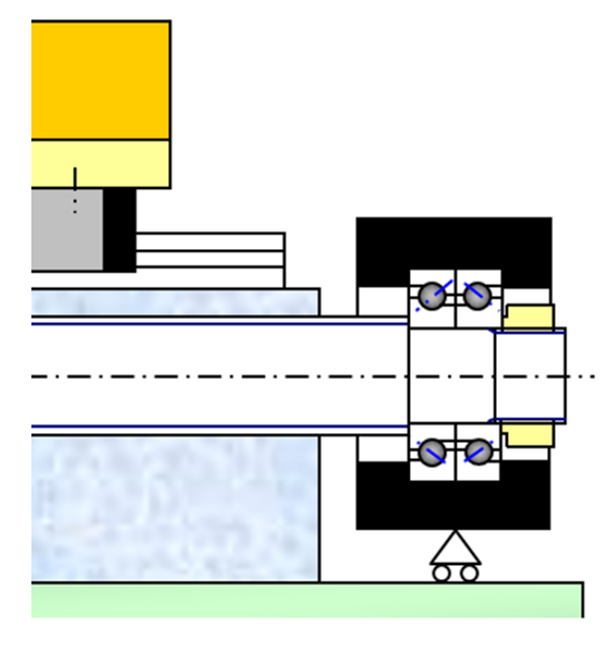
図6 ねじ軸の伸びの測定を考慮した予備実験の力学的構成例
以下の各章では、SSMを用いた軸力の安定的維持の根幹となる圧力室における内圧のモデル化とそれにもとづく計算結果の検証、さらには実際のボールねじ送り系の構成を対象としたSSMの仕様検討プロセスについて述べる。
3. SSMの圧力室で生じる内圧のモデル化と張力の維持効果
3.1 SSMの圧力室における内圧のモデル化
図7にSSMを取り付けた実験用のボールねじ送り系、表1にこの装置の仕様を示す。図8はこの装置をATC(Automatic Tool Changer)による工具交換を含む金型加工サイクルに相当する条件で約4時間にわたり送り運動のみ加工サイクル稼働させ、サイクル停止後も含めてSSMの圧力室内における圧力変化を測定した結果である。ここではSSMの内部構成について、『条件A:作動油のみ封入』と『条件B:作動油と中空ばね要素を封入』を設定して実験を行った。圧力室内の圧力は圧力計により、ねじ軸の変位については軸受の抑え蓋に機台側から電気マイクロメータを接触させて計測している。なお実験装置の組立にあたっては、多くのボールねじ送り系に適用されている3ºC分の熱膨張に相当する伸びを与える予張力を付与することとした。実験用のボールねじ送り系においてこの力を発生させる圧力室内の内圧は1.3 MPaであり、サイクル稼働中を含め同圧力がこの近傍の1.0~1.5 MPaを維持していることが明らかとなった。
図8の結果を詳細にみると、両条件において内圧が初期状態(1.1 MPa)から稼働時間とともに上昇していることがわかる。特に作動油のみが封入された条件Aにおいて圧力が大きく変化しており、4 時間経過後には初期の約1.6倍に達している。この結果は、圧力室内の作動油の温度が大きく上昇したためであると考えられる。一方、作動油に中空ばね要素を内包させた条件Bにおいては、圧力の上昇が緩やかで、4時間経過後の圧力は初期の1.1倍程度である。これは、中空ばね要素の存在により、作動油の温度上昇による圧力室の内圧変化が抑制されたためであると考えられる。
SSMの仕様検討においては、作動油の温度上昇による内圧の変化を抑制するように中空ばね要素が効果的に機能することが重要である。そこで本研究では、SSMの最適設計を目的として圧力室内で発生する圧力の計算手法の構築に取り組むこととした。
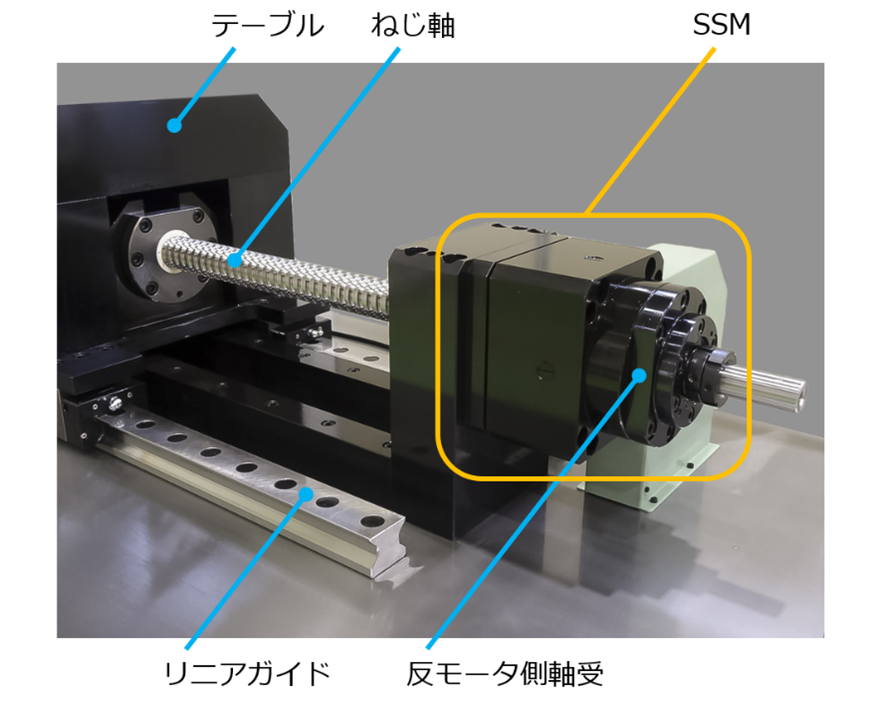
図7 SSMを搭載したボールねじ送り系の実験装置

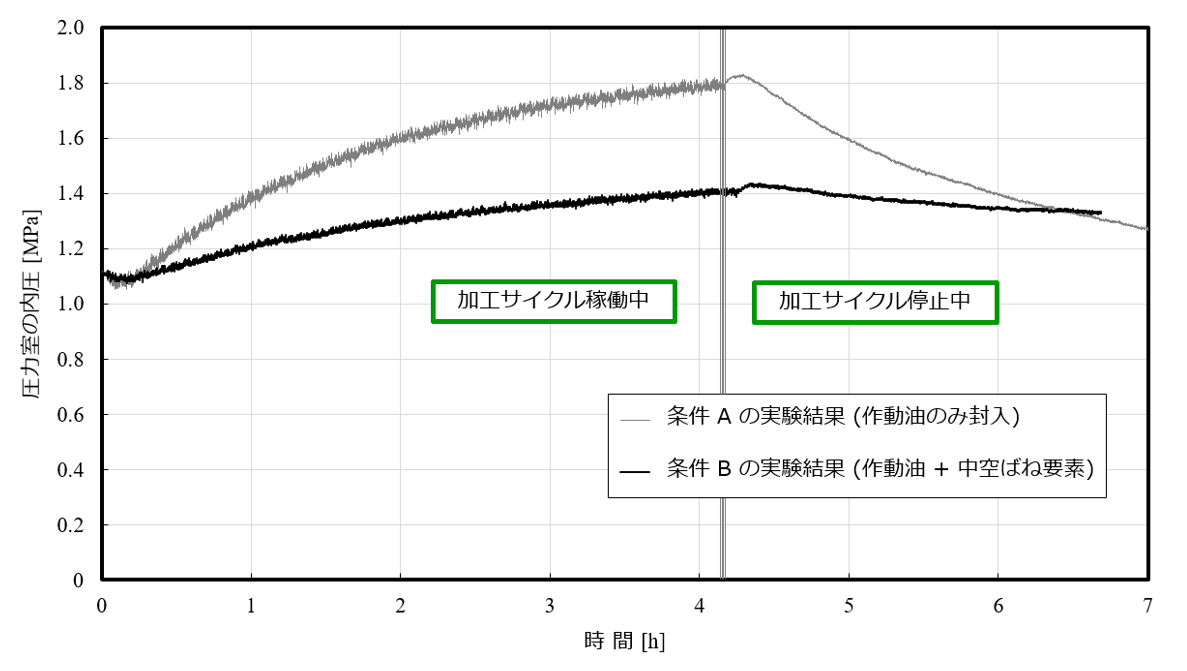
図8 ボールねじ送り系を対象とした実験での圧力室における内圧の変化
先述のように、SSMは作動油とこれに比べて相対的に柔らかい中空ばね要素によって、圧力室の内圧変化を抑制していると考えられる。そこで本研究では、圧力室内を図9に示すような直列ばねとしてモデル化した。ばね1とばね2は、それぞれ作動油と中空ばね要素を表している。ばねのピストン側は機台に固定される一方で、シリンダ側はねじ軸の線膨張に従ってシリンダとともに動くことができるものとする。
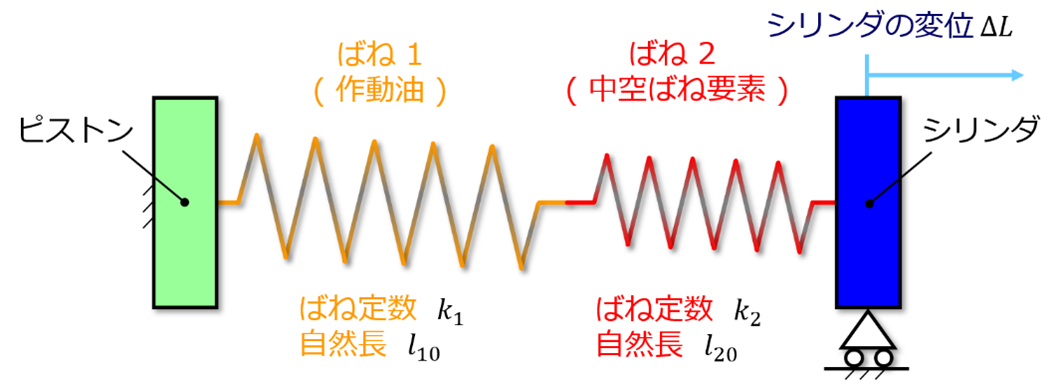
図9 圧力室における作動油と中空ばね要素の力学的モデル化
まず、 ばね1およびばね2のばね定数をそれぞれk1、k2とすると、直列に接続されたモデル全体のばね定数kは以下のように表せる。

一般に作動油の体積弾性率は約1,500 MPaであり(中川、大住、1976)、空気の体積弾性率(約0.1 MPa)よりも極めて大きい。よって空気を内包する中空ばね要素を適切に設計することで、モデル全体のばね定数kを制御して、SSMの内部で生じる圧力の変化を抑制することができる。
この場合、温度一定の条件下でシリンダの変位ΔLによりモデル全体に生じる力は、以下のように表せる。

一方でシリンダが固定された条件下で温度がΔT変化したとき、モデル全体にはふたつのばねの膨張分α1 ∆Tℓ10+α2 ∆Tℓ20に対応する力Fが発生する。ここでα1、α2はそれぞれをばね1とばね2の線膨張係数、またℓ10、ℓ20はそれぞればね1とばね2の自然長とする。
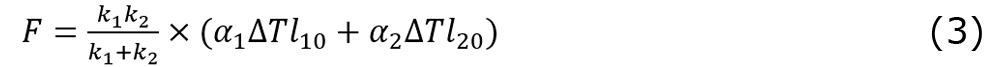
図10は、図8において示した条件Bの実験における各部位の温度、ねじ軸の伸び、圧力室における内圧の変遷を示したものである。図10(a)によれば、SSMの各部位における温度上昇は最高でも4時間で13℃程度と非常に緩やかであることから、ここでは作動油と中空ばね要素の温度は等しいと仮定している。
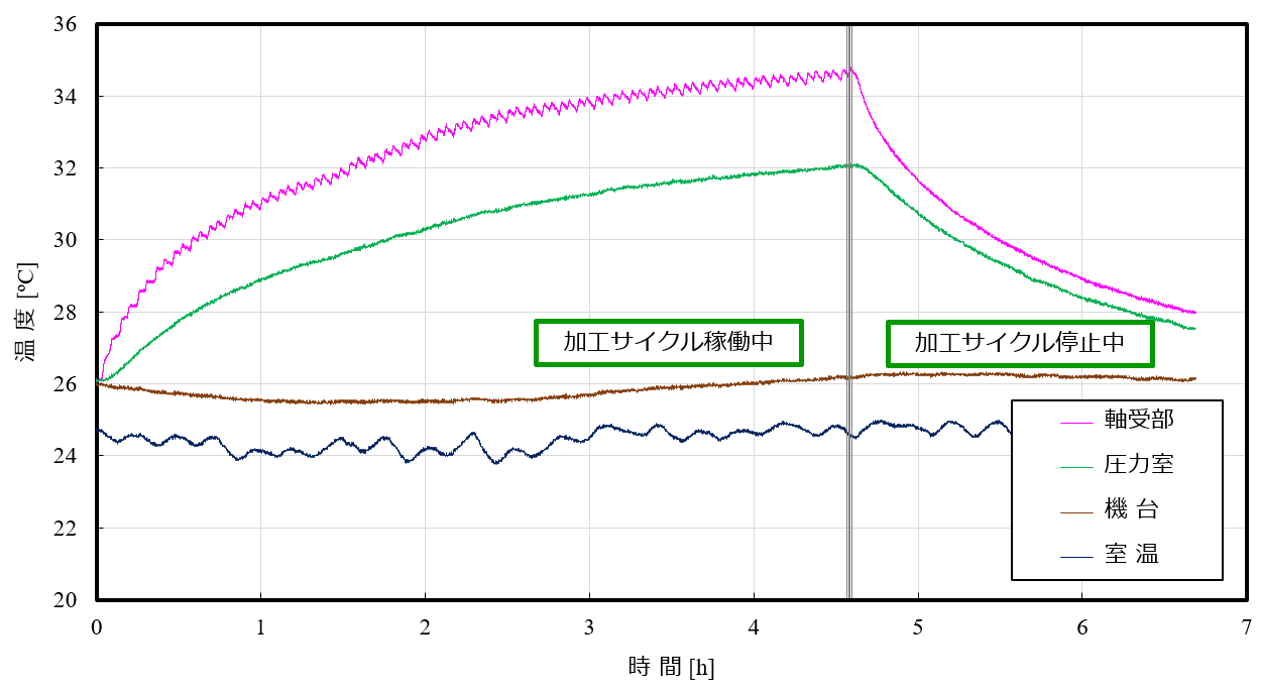
(a) 各部位の温度の変遷
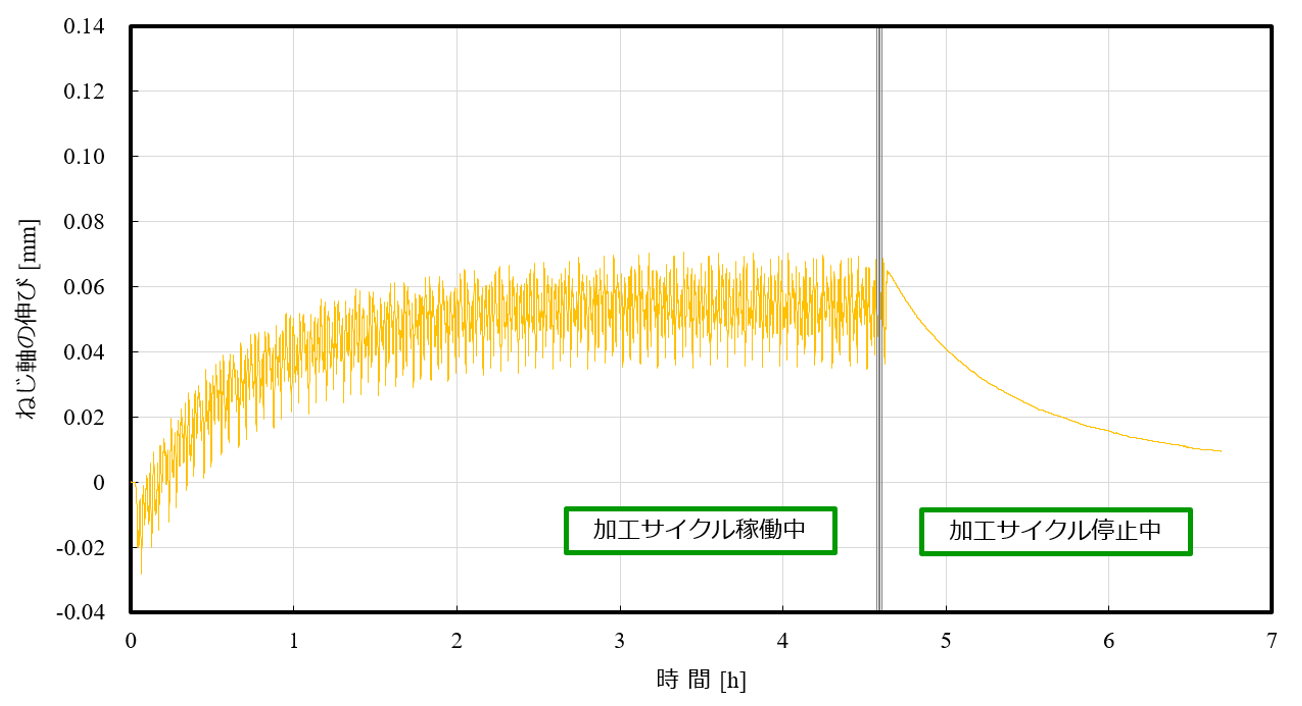
(b) ねじ軸の伸びとの内圧の変遷
図10 条件BのSSMを搭載したボールねじ送り系で得られた実験結果
式(2)、(3)を用いると、シリンダの変位ΔLと温度変化ΔTによってモデル全体に発生する力Fは以下のように表せる。
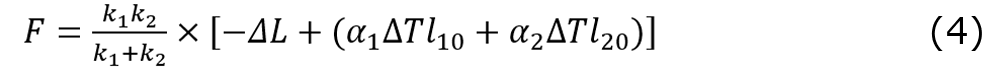
式(4)からは、ねじ軸の線膨張による変位の効果と温度変化の効果が互いに打ち消し合っていることがわかる。
続いて、上述の1次元ばねの直列モデルを3次元の圧力室内で発生する圧力の式に拡張する。圧力室全体の体積Vは作動油および中空ばね要素それぞれの体積v1およびv2の和で表せるため、その変化は以下のように記述できる。

体積Vを圧力と温度の関数V(T、P)で定義すると、Vを構成する各項の変化量は次のように表せる。
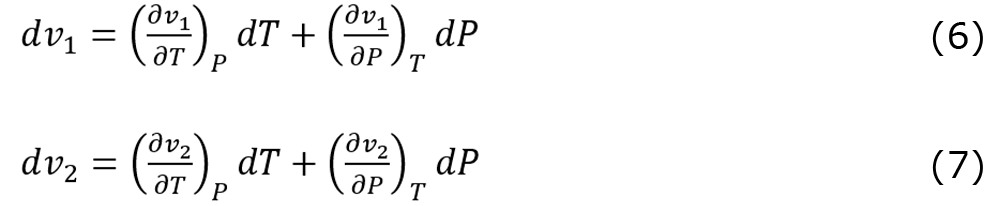


以上を用いると、圧力室全体の体積変化 dP は次のように表せる。
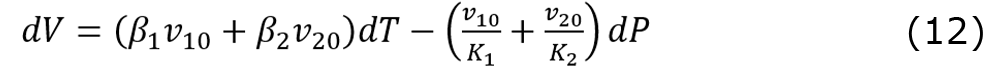
これを圧力室で生じる内圧変動 dP について整理すれば、以下の式 (13) が得られる。

ここでV0は圧力室の初期体積を表しており、v10とv20の和で定義されるものである。
式(13)の第1項は圧力室の体積変化の影響を表しており、第2項は圧力室内の温度変化による影響を表している。
なお本研究において作動油の体積弾性率K1は、条件Aのシリンダをゆっくりと変位させ圧力と体積の関係を測定することで決定した。また作動油の体積膨張率β1については、条件Aの加工サイクル稼働実験の結果と一致するように決定した。
他方中空ばね要素の体積弾性率K2および体積膨張率β2に関しては、中空ばね要素の形状と材料物性によって決まる値として定義できる。3.2では、これらの中空ばね要素に関する特性の取り扱いについて述べる。
3.2 中空ばね要素の構成と物性値の導出
式(13)により圧力変化を計算するためには、作動油のみならず中空ばね要素の体積弾性率および体積膨張率の導出が必要となる。これらの値は中空ばね要素の形状および材料物性に依存するため、送り系の仕様や使用条件に合わせた十分な検討が必要になる。本研究では、これらの値をFEM解析を用いて見積もることとした。
図11に中空ばね要素の解析モデルを示す。今回対象とするSSMの圧力室はねじ軸が中心部を貫通する円筒空間で構成されている。従って中空ばね要素の形状は、リング状の軸対称モデルで構築した。解析においては、中空ばね要素が3℃分の予張力に相当する1.3 MPaの内圧が圧力室内で発生した場合であっても壊れないこと、密封性や耐久性の観点でも機能を達し得ることを設定条件として材料には樹脂を用いることとし(志村、1999)、その外壁に圧力を与えた際の圧力と体積変化の関係を算出した。
図12には、FEM解析によって得られたリング状中空ばね要素の変形状態を示す。この図から、周囲に存在する作動油からの圧力によって特に中空ばね要素の上下面が凹むように変形して、中空ばね要素全体の体積が減少していることがわかる。
本研究では、この結果をもとに作動油から受ける圧力と中空ばね要素の体積ひずみの関係を求め、中空ばね要素の体積弾性率K2を導出した。また中空ばね要素の体積ひずみと同要素内で発生する圧力の関係については、形状および物性に関する検討を行い線形関係が得られるように選定した。なおSSMでは作動油の温度が変化する範囲が13℃程度までであり、この範囲では樹脂材のヤング率がほとんど変化しないことから、体積弾性率K2は温度によらず一定であると仮定した。中空ばね要素の体積膨張率β2は、作動油の体積膨張率β1に対して十分小さいため無視することとした。
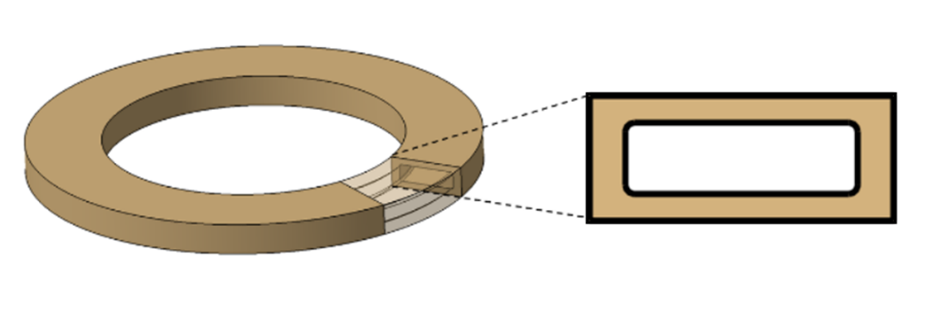
図11 リング状中空ばね要素の解析モデル
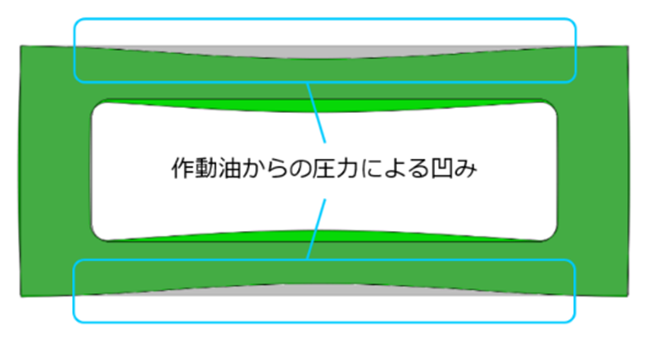
図12 リング状中空ばね要素の変形のFEM解析結果
3.3 圧力室における内圧モデルの妥当性の検証と考察
圧力室における内圧モデルの妥当性を検証するため、式(13)を用いた計算結果と図8に示した条件Bの実験結果を比較した。図13に条件Bの計算と実験の結果を示す。ここでは条件Aにおいて推定した体積膨張率β1をもとにして条件Bの計算を行っていることから、前提となる条件Aの実験結果とβ1を反映させた計算結果も併記した。モデルの妥当性を確認するため、ねじ軸の伸びと圧力室の温度変化には、それぞれ実験から得られた測定値を入力している。
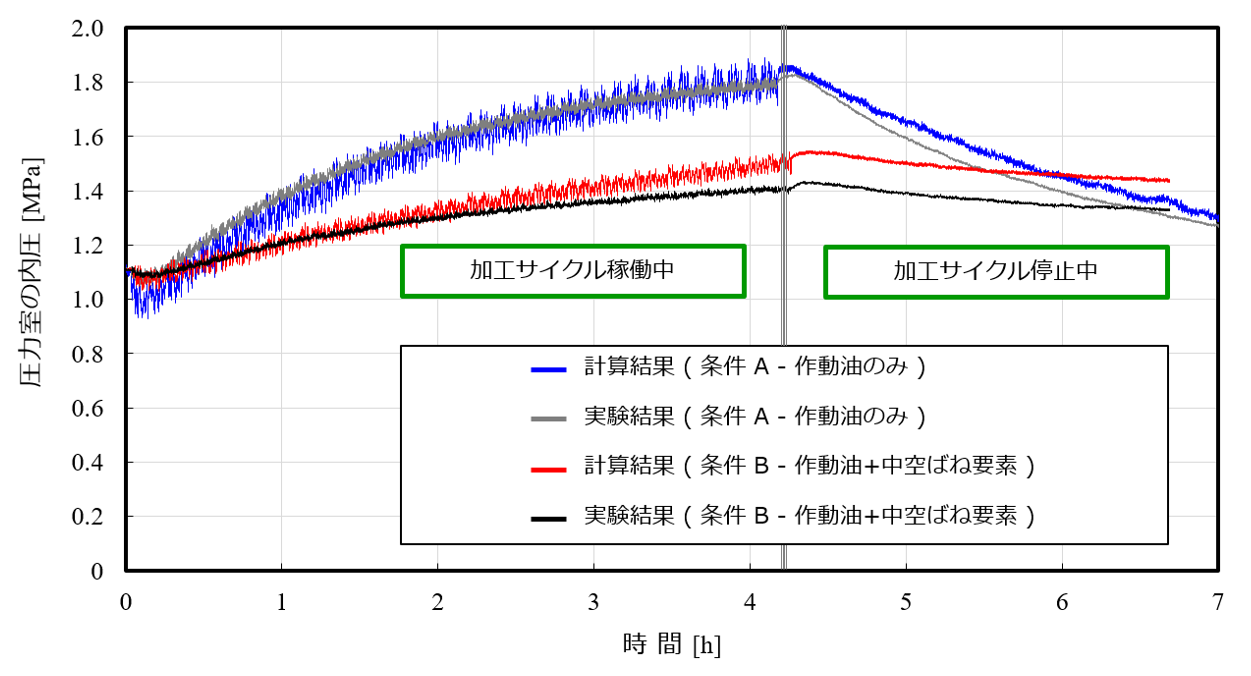
図13 条件BのSSMを搭載したボールねじ送り系における内圧の計算と実験の結果
内圧変動の傾向を見ると条件Bの計算結果は実験結果とよく一致しており、構築したモデルが妥当であることがわかる。
なお条件Aと条件Bにおいて加工サイクル稼働中の内圧上昇時に微小な圧力の周期成分が見られるが、これは実験において送り系のテーブル移動方向が変化した際にねじ軸を介してSSMのシリンダに伝わる内力の変化により生じる影響であることが確認されている。これを踏まえて条件Aと条件Bの内力の周期成分の振幅の大きさを比べると、条件Aの方が条件Bよりも大きくなっていることが見て取れる。条件Aには中空ばね要素が用いられていないことから、これはテーブルからねじ軸を介してSSMの圧力室内に封入された作動油に伝わる送り系の運動起因の内力の微小な変化がダイレクトに顕在化したものと考えられる。同様の視点で条件Bの傾向を見ると、計算と実験の両者において内圧の変化成分における振幅が小さくなっていることがわかる。すなわち圧力室に作動油と中空ばね要素を封入した構成には、内圧の変化を軽減する効果があると捉えることができる。
4. ボールねじ送り系構成時におけるSSMの仕様検討
SSMの圧力室における内圧モデルの構築ならびに計算と実験の結果に関する検証が同モデルの妥当性を明らかにしたことを踏まえて、図5に示す張力の計算アルゴリズムの適用を前提としたボールねじ送り系構成の際のSSMの仕様検討プロセスを考案した。
前述の通り、ボールねじ送り系にSSMを搭載する場合、圧力室内において発生する内圧を計算するためには、入力値として時々刻々のねじ軸の伸びと圧力室内に封入した作動油の温度変化といった2つの情報が必要になる。図13に示した計算と実験の結果比較においては、計算アルゴリズムの妥当性を検証するため、条件Bを対象にこれら2つのデータとして実験から得られた測定値を用いて計算への入力値とした。しかしながら実際のSSMの仕様検討においては、これら2つのデータは送り系の構成とリンクするかたちで適切に推定される必要があり、これらがなければSSMの圧力室の詳細設計は滞ることになる。その一方で、これらの情報は送り系の構成、加工サイクル、環境の影響を受けるため、汎用性を持つように定式化することが極めて難しい。
よって本研究では、SSMの圧力室内を大気に開放した状態を設定した送り系において図6に示す力学的な構成のもと発熱体としての軸受がSSM設置時の予圧と同一になるように配慮しつつ、この部位で発生する熱量が継続的にねじ軸の伸びに影響を与える構造をSSMの仕様検討段階で実践的に設定する対応策を立案した。そのうえでこの構成における加工サイクル稼働実験を予備実験と定義することで、SSMの仕様を決めるための前提となるデータを取得した。
予備実験において加工サイクル稼働したときのねじ軸の伸びは、『ねじ軸が力学的に安定した状態で素直に伸びる理想的な熱変形モード』と考えることができる。これはすなわち、予備実験で得られたねじ軸の時々刻々の伸びデータがSSMを搭載した送り系を構成した際でもねじ軸の伸びの目標値になることを意味している。なお圧力室内の作動油の温度については、予備実験で設定した構成において圧力室に対応する位置で温度を測定し入力値とした。これらのデータは内圧計算の際の入力値として計算精度に大きな影響を与えるため、実験的に取得することでSSMの圧力室で発生する内圧解析結果の信頼性を高める効果をもたらすと考えられる。
予備実験から得られた実験データの結果を、図14に示す。図14(a)には予備実験から得られた軸受部・圧力室・機台の温度と室温の測定結果、また図14(b)には、予備実験で測定したねじ軸の伸び量をプロットしている。

(a) 各部位の温度の変遷

(b) ねじ軸の伸びの変遷
図14 予備実験で得られた結果
図15は、図14(a)に示した予備実験をベースとする圧力室内の作動油温度および図14(b)に示したねじ軸の伸びのデータを入力値として用いてSSMの仕様検討を行った結果を、内圧の計算と実験の結果の変遷で示したものである。仕様検討の過程では、圧力室に封入すべき作動油量や中空ばね要素部材の諸元を変化させ、設計条件を選定している。そのうえで最終的には、加工サイクルによらず圧力室で発生する内圧の変動を低減するように設計を行っている。
図15によれば、計算と実験の結果が似通った性質、すなわち時間が経つにつれて圧力変動が飽和する経過や初期の内圧に対する圧力の変動成分の割合などがほぼ一致する傾向を示していることがわかる。これらの傾向は、予備実験により得られるねじ軸の伸びを基準値とするとともに圧力室の温度を作動油温度と見立てて用いたSSMの内圧を計算する一連のプロセスの有効性を示している。言い換えれば、ボールねじ送り系全体を網羅した熱収支を見積らなくても、ねじ軸の伸び量を幾何学的拘束条件として捉え軸端部における発熱状態やその熱の流れに注目してSSMで発生し得る内圧をモデル化すれば、ねじ軸に作用する張力を安定的に維持する設計仕様を見出し得るという本研究の提案が、実践的に適用可能であると証明していると捉えることができる。
図16は、図15に示した圧力室の内圧の実験結果をねじ軸の伸びとともに表しつつ、3ºC分のねじ軸の伸びに対応した予張力を付与した従来構成のボールねじ送り系においてねじ軸内で発生する引張り応力を、SSMを構成する圧力室の設定を仮定した際につりあう等価圧力に換算したうえでプロットしたものである。この結果からは、予張力を与えた送り系ではねじ軸が80 μm程度伸びるのに対応できず30分弱で早々と軸力を失う一方で、SSMを搭載した送り系ではねじ軸が3ºC分の予張力付与の制約以上に伸長する場合であっても安定的に軸力を維持していることがわかる。このことは後者において送り系の力学的な特性が変わらないことを示しており、ねじ軸の冷却や機械自体の熱的な状態を安定させる暖機運転の排除、すなわちコールドスタートの実現可能性を示唆していると捉えられる。よってSSMを搭載した送り系では、位置決め精度を保証し得る適切な付帯機能(例えばリニアスケールによるフルクローズドループ機能)を構成すれば、送り系の機能の経時変化に留意しなくても高精度な機械加工を継続的かつ安定的に実現できると考えられる(横山他、2008;坂本他、2019;曽我部他、2020)。
また図16によれば、送り系の加工サイクルの稼働が停止した後にねじ軸が収縮する範囲においても、圧力室内における内圧が維持されていることが見て取れる。この傾向から、本研究で提案した圧力発生のしくみならびにその内圧モデルがねじ軸の線膨張時のみならず収縮時にも有効に機能することがわかる。言い換えれば、圧力室を対象とした内圧モデルはSSMの特徴である『エネルギーの循環機構』としての機能を適切に表しており、汎用的に適用可能な考え方を提示していることを裏付けるものであると考えられる。
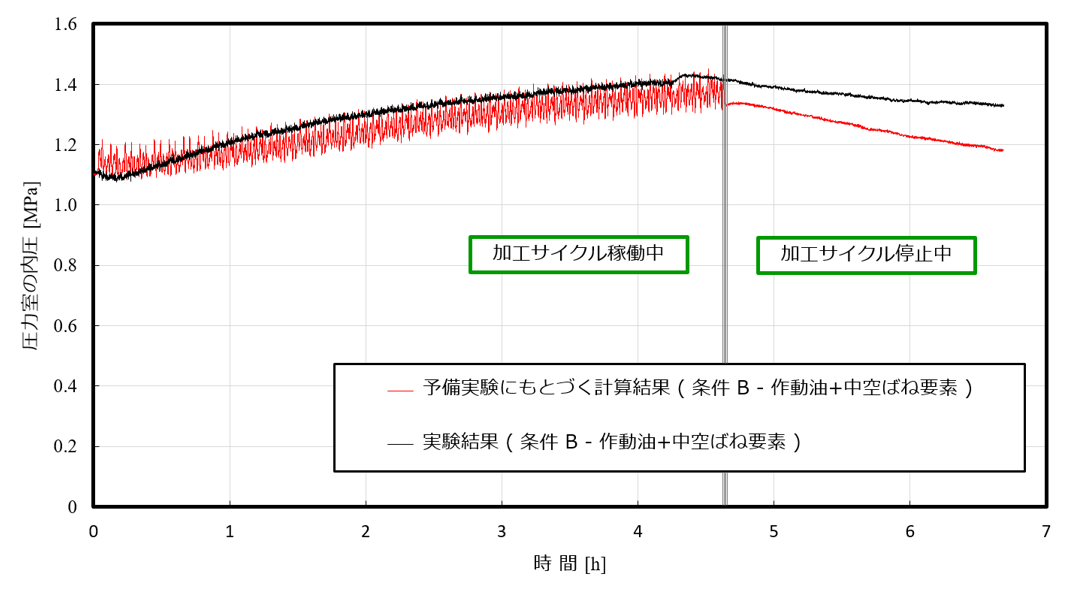
図15 予備実験にもとづく圧力室内の内圧の計算と実験の結果
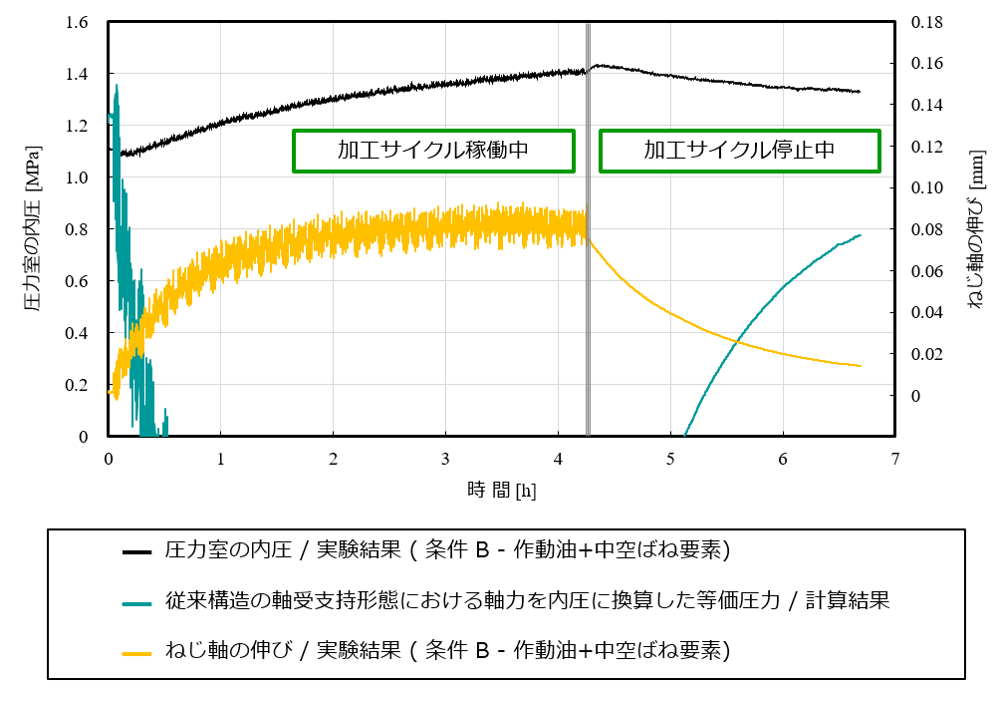
図16 圧力室の内圧とねじ軸の伸びの関係
5. 結言
工作機械に搭載されるボールねじ送り系において発熱によりねじ軸が伸長する現象は、これまでは主に加工精度に影響をもたらす課題として捉えられ、その対策は冷却による構造的な変形の抑制やねじ軸への予張力の付与による限定的な剛性の保持にフォーカスしたものが主流であった。
しかし省人化や環境負荷低減が待ったなしとなっている昨今、発熱による状態変化を属人的なやり方で凌いでいる対処療法が完全なかたちでの自動化を阻んでいること、発熱の影響を阻止するため二次的なエネルギーを投入して冷却したり恒温室を設定するなどの環境に負荷を与える方法が認められにくくなりつつあることなどの世情を背景として、これらの課題を抜本的に解決することが求められるようになってきた。
本研究では、このような要望に対して機械設計の観点から本質的な改善策を示すことを目的として、ねじ軸の発熱による伸長をあるがままに受け入れるとともに、伸長しても軸力が安定した状態を維持できる状態安定化機構(State stabilization mechanism to maintain axial tension:SSM)を開発した。本稿では特にSSMの基本機能に絡んで、そのしくみ、ユニット内の圧力室における内圧のモデル化、内圧維持に関する検証結果、実際に送り系を構成する際の仕様検討プロセスについて述べた。
本研究で得られた成果をまとめると、以下のようになる。
- ボールねじ送り系のねじ軸を支持する軸端部に軸受を内包するシリンダとピストンからなるSSMを取り付けることで、ねじ軸が発熱により伸長しても継続的に安定した軸力を得る方法を提案した。
- SSMの内部にピストンとシリンダの勘合部に作動油と中空ばね要素を封入した圧力室を設けて、軸受から流入する熱をエネルギー源として作動油を膨張させつつ、中空ばね要素の内圧調整機能と相まって張力を安定維持するこれまでにないエネルギー循環のしくみを構築した。
- SSMの内部に構築した圧力室における内圧発生のメカニズムを作動油と中空ばね要素それぞれをばねで記述したうえで、それらを直列配置したモデルで定義した。実験結果をもとにしたねじ軸の伸びと作動油の温度を入力情報として用意したうえで提案したモデルから内圧変動を計算したところ、実験値に近い傾向を確認することができた。
- 送り系を構成する段階でSSMに求められる設計仕様を明らかにするため、対象とする送り系上において軸受部で発生する熱がねじ軸の伸びに影響を与える構造を構成したうえでねじ軸の伸びと作動油の温度に関するデータを予備実験から取得するプロセスを提案した。この実験から得られた情報をもとに入力値を準備する取り扱いにより、実践的かつ汎用的なSSMの仕様検討が可能になることを示した。
- 計算および実験の結果から、従来熱膨張に対応するため3ºC分の伸びに相当する予張力を付与していた設計仕様の限界を超えてねじ軸が伸長した場合であっても、SSMを搭載した送り系ではねじ軸に軸力が安定的に作用し続ける状況をもたらし得ることを明らかにした。またねじ軸の伸長時のみならず収縮時にも圧力室における内圧の安定性が見て取れる傾向から、構築した圧力室の内圧モデルが『エネルギーの循環機構』としての機能を適切に記述していることがわかった。
今後は本研究で得られたSSMがもたらす張力維持の機能をベースとして、ボールねじ送り系の剛性や減衰能をはじめとする機械特性に与える効果、SSMを搭載した送り系の制御性、加工現象への影響などについても定量評価を行い理論構築に努めていく所存である。
参考文献
1) Altintas Y., Verl A., Brecher C., Uriarte L. and Pritschow G., Machine tool feed drives, CIRP Annals, Vol. 60, No. 2 (2011), pp.779-796. DOI:10.1016/j.cirp.2011.05.010
2) Arai S., Wilson S. A., Corbett J. and Whatmore R. W., Ultra-precision grinding of PZT ceramics–Surface integrity control and tooling design, International Journal of Machine Tools & Manufacture, 49 (12-13) (2009), pp.998-1007.
3) Bryan J., International status of thermal error research, Annals of the CIRP, Vol. 39, No.2 (1990), pp.645-656. DOI:10.1016/S0007-8506(07)63001-7
4) 稲垣孝洋, 松原厚, 河野大輔, 接触剛性が工作機械の支持剛性に与える影響に関する研究, 精密工学会秋季大会学術講演会講演論文集 (2011), pp.413-414.
5) Inasaki I., Machining processes in precision engineering, Klocke F. and Pritschow G. / Autonome Produktion, Springer (2004), pp.27-37.
6) 垣野義昭, 森一晃, 夏書強, 木本康雄, 森山浩光, 東本暁美, NC工作機械におけるボールねじの熱変位補正, 精密工学会誌, Vol. 54, No. 9 (1988), pp.1753-1758. DOI:10.2493/jjspe.54.1753
7) Mayr J., Jedrzejewski J., Uhlmann E., Donmez M. A., Knapp W., Härtig F., Wendt K., Moriwaki T., Shore P., Schmitt R., Brecher C., Würz T. and Wegener K., Thermal issues in machine tools, CIRP Annals, Vol. 61, No.2 (2012), pp.771-791. DOI:10.1016/j.cirp.2012.05.008
8) 水口淳二, 永井豊, 山本和史, ナット冷却ボールねじの開発, NSKテクニカルジャーナル, No.687 (2015) pp.45-49.
9) 中川孝之, 大住剛, 混入空気を考慮した油圧作動油の体積弾性係数について, 富山大学工学部紀要, Vol. 27 (1976), pp.25-30. DOI: 10.15099/00004177
10) 二宮瑞穂, ボールねじの摩擦と温度上昇, NSKテクニカルジャーナル, No.637 (1978), pp.9-16.
11) 二宮瑞穂, 宮口和男, ボールねじの最新技術動向, NSKテクニカルジャーナル, No. 664 (1997), pp.1-13.
12) 小渕信夫, 大塚二郎, 星野高志, ボールねじの熱膨張に関する研究: 差分法による温度分布計算, 精密工学会誌, Vol. 53, No. 12 (1987), pp.1899-1904. DOI:10.2493/jjspe.53.1899
13) 坂本潤嗣, 寺島重夫, 小林武夫, 熱変位補正システム用基板の開発, 長野県工業技術総合センター 環境・情報技術部門研究報告, No.14 (2019), pp.E23-E26.
14) 千田治光, 森脇俊道, 工作機械ボールねじの熱変形による加工誤差の抑制に関する研究, 日本機械学会論文集C編, Vol. 72, No. 717 (2006), pp.1667-1672. DOI:10.1299/kikaic.72.1667
15) 清水伸二, 城石利和, 坂本治久, 結合面接触剛性のFEM解析への組み込み法 (第2報): 結合構造体の非線形変位挙動解析による妥当性の検討, 精密工学会秋季大会学術講演会講演論文集 (2005), pp.21-22. DOI:10.11522/pscjspe.2005A.0.21.0
16) 志村幸雄, プラスチック・データブック, 旭化成アミダス株式会社「プラスチック」編集部編, 工業調査会 (1999)
17) 曽我部英介, 溝口祐司, 千田治光, 工作機械におけるプリテンションを付加したボールねじの熱変位補正, 精密工学会春季大会学術講演会講演論文集 (2020), pp.830-831. DOI:10.11522/pscjspe.2020S.0_830
18) Weck M., Handbook of machine tools Vol. 2 / Construction and mathematical analysis (translated from the original German by Bibring H.), John Wiley & Sons (1984)
19) 横山和宏, 小寺岳彦, 永井豊, 鈴木孝昌, 熱膨張量推定のためのボールねじ温度分布測定位置の選定, 設計工学, Vol.41, No.8 (2006), pp.37-42.
20) 横山和宏, 斉藤瑞希, 鳥海啓, 森脇俊道, 明田川正人, ボールねじ熱膨張のリアルタイム補正による位置決め精度の向上 (第1報): 補正の原理と運転条件の影響, 精密工学会誌, Vol. 74, No. 9 (2008), pp.931-936. DOI:10.2493/jjspe.74.931
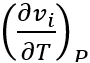 は、圧力一定条件での温度変化に対する体積の変化率である。作動油および中空ばね要素それぞれの体積膨張率β1およびβ2、作動油および中空ばね要素それぞれの初期体積v10およびv20を用いると、
は、圧力一定条件での温度変化に対する体積の変化率である。作動油および中空ばね要素それぞれの体積膨張率β1およびβ2、作動油および中空ばね要素それぞれの初期体積v10およびv20を用いると、